PinephonePro with Gentoo

2023-03-22

In this post I'm going to skip the why and jump to the what. I crosscompiled Gentoo for my Pinephone Pro with Pinephone keyboard, and got it working pretty nicely, and I wanted to document some of the process for others.

Obligatory photo of phone in operation

In retrospect the easiest path to get close to what I'm running would be to install mobian and then just use sway instead of phosh etc. One advantage of Gentoo though is the ability to run wayland-only which saeves on resources. An easier way to get Gentoo would be to just download an arm64 stage 3, downlad a mobian image, replace the userland with the stage3 tarball, and you'd be most of the way there. That is not the path I took though. One downside of that approach is that you aren't left with a matching cross-compiler environment for building packages requiring more than the 4GB of ram on the Pinephone Pro. Whether it's worth the extra effort, is up to you.

What is this post's purpose? I'm an experienced software engineer and long-time Linux user and admin. I've run Gentoo in particular before, and recently came back to it. That said, this was my first time building or using a cross-compiler or doing any sort of project like this. My target audience is folks similar to myself. The following is not intended as instructions for beginners. It's an approximate outline that I hope can help others with similar experience avoid a lot of dead ends, and many many hours of googling, or enable someone with a bit less knowledge to pull this off at all.

I'm kind of joking, but so far I haven't tried to get GPS, or the cell modem to work. My priority was to make it useful like a laptop. I have tried to get the camera to work. The client software is called "Megapixels". It installs fine, and I've heard works on the pinephone, but the pinephone pro needs some kernel patches that are not widely used yet. I DO have full convergence working with the kernel config I posted. I can use a USB or bluetooth keyboard, a USB-C HDMI hub, an external HDMI monitor, a USB keyboard, and an ethernet device built indo the USB-C hub, and it all works great. My bluetooth headphones work well, my USB headset works fine. I have the power-button suspend via elogind. My volume buttons work. I can change screen brightness with keyboard shortcuts. If you DO use my config and do anything I don't, you'll probably need to enable those features :).

Honestly, if you manage to truly brick your phone I'm impressed, it's not easy with the pinephone pro... but should you pull it off you're doing this at your own risk, I'm not liable, not my fault, bla bla bla. This just my blog. I don't know what I'm doing.

obligatory photo of pinephone pro doing convergence stuff

Pinephone Tips

At this point hopefully you have gentoo booting on your pinephone. But that's a ways from having everything you want working. Since we've basically set up the pinephone like a laptop you can test things out on a laptop and then apply the changes to your pinephone if that's helpful. But here's some ideas

As I mentioned I'm using wayland only swayWM. Some software I like

I'm hoping to write up another post about my desktop configuration and using sway soon, for less pinephone specific information. But there you go.

This is not the easiest process, but compared to your average "build your own OS for arbitrary device" project I suspect this is downright trivial. If you're good with linux and understand how it all works this actually isn't all that hard. I had to do a lot of reading to e.g. work out what the cflags should be, which bootloader to use, the best way to get a bootable system, etc. Hopefully this set of psuedo-instructions will save you those headaches and make the project only a little more involved than a typical gentoo install.

Lastly, other people blazed this trail already. First the all the folks who patched the Linux kernel, wrote firmware for the pinephone keyboard, etc. And then folks who build Gentoo for it before me. I just followed in there footsteps. https://gitlab.com/bingch/gentoo-overlay/-/blob/master/README.md is the best resource I found https://xnux.eu/howtos/build-pinephone-kernel.html Is where I found megi's sources (though I ended up using the ones from bingch). Megi did a lot of the work of writing patches and collecting disprate patch sets together to get the pinephone to really work well. I know I used a couple of other sources for gentoo-specific pinephone knowledge, but have forgotten what they worry, so appolagies for not citing you, whoever you are.

String Sorts

2019-01-23

You'll recall in my recent post about Fast Sort we learned that Radix Sort is significantly faster at sorting 32 bit integers than normal comparison based sorts, particularly as the array gets large. A result every computer scientist knows theoretically, yet with median-find we saw how theoretical bounds don't always translate in practice.

Well, a friend asked me, what about sorting variable length strings? Does radix sort still beat comparison based sorts? It's a fair question so, I decided to take a shot at it. And here are my results:

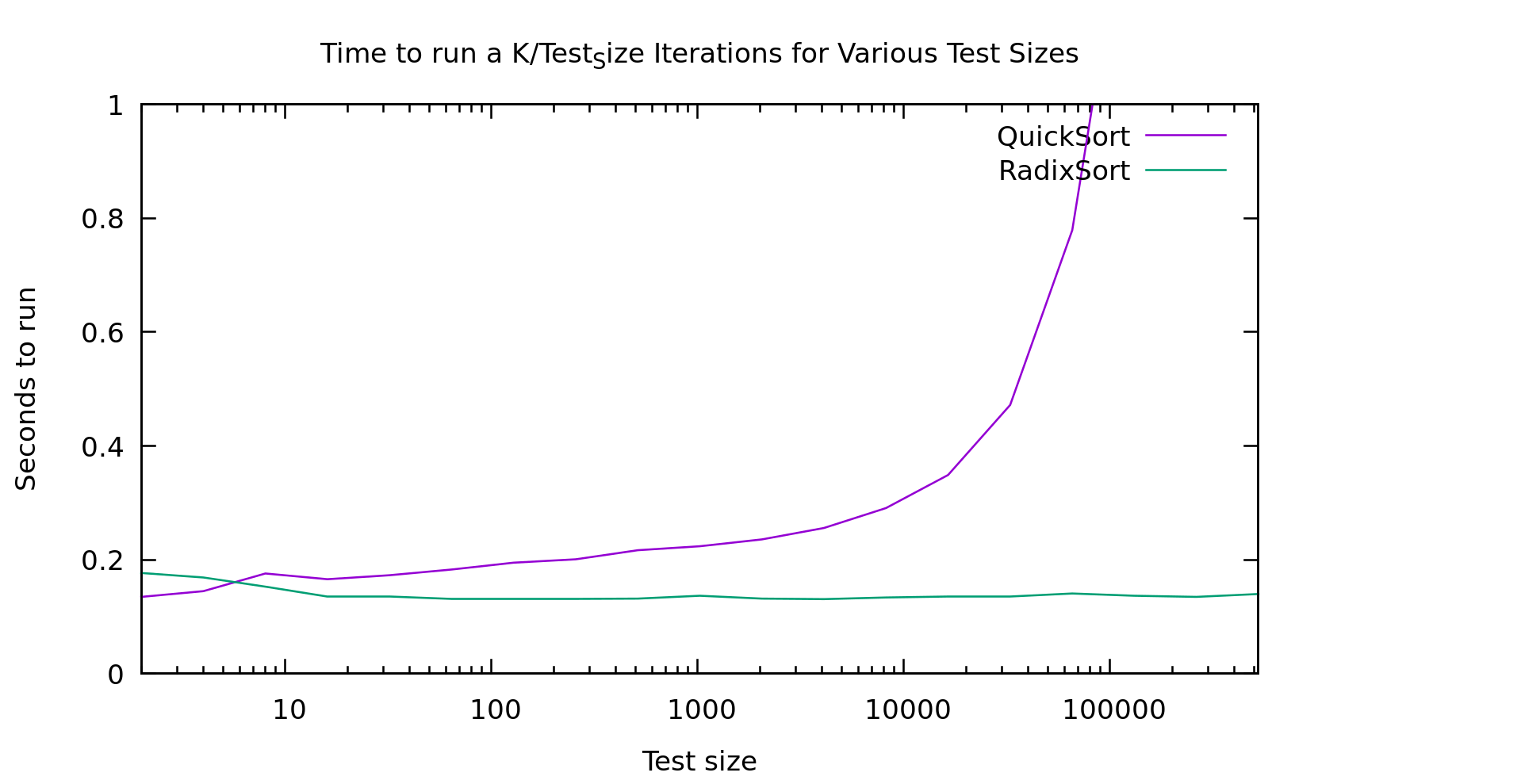
In my mind that graph is pretty clear, above 10 elements radixsort is clearly winning. Note that this is currently a 128 bit radix-sort that only handles ASCII... though I'm actually only feeding it uppercase strings currently. So, lets talk about how this algorithm works, because it's not an entirely trivial conversion of radixsort

String Radix Sort Algorithm

This is a little bit interesting. You may recall that there are two types of radix-sort. Least Significant Digit first, and Most Signicant Digit first. These are referred to as LSD and MSD. My binary radix sort from earlier benchmarks was an example of an MSD sort, and the one I just referred to as "radix sort" is an LSD sort. LSD sorts are preferred generally because they are stable, simplier to implement, require less temp space AND are generally more performant.

There's just one problem. With variable length strings, LSD sorts don't work very well. We'd have to spend a lot of time scanning over the array just looking for the longest array so we can compute what counts as the smallest significant bit. Remember that in lexicographic ordering it slike all the strings are left justified. The left-most charactor in each string is equivelent in precidence, not the rightmost.

MSD sorts, must be recursive in nature. That is, they need to work on only the sublist we sorted in to a certain bucket so far. I'm going to call this sublist a "slice". To keep our temporary space vaguely in order I'm using a total of 5 lists.

Here's the algorithm. Start by looking at the first bytes of the strings. Look in slice list A, and get the next slice. Bucket everything in this slice. Each of these buckets (if non-empty) becomes a new slice, so write strings back out to string list B, and write the index of end each slice in to string list B. Swap lists A and B, move to the next byte, and do it again. We terminate when for each slice it's either of length 1, or we run out of bytes. To see the full implementation take a look at string_sort.h in my github repo .

Conveniently, they way my algorithm works it is in fact stable. We walk the items in order, bin them in order, then put them in the new list still in order. If they are equal there is no point where they'd get swapped.

It's a LOT of temporary space, which is kind of ugly, but it's pretty performant as you saw above. Another optomization I haven't tried is short-circuiting slices of length 1. We should be able to trivially copy these over and skip all the hashing work. Testing would be required to see if the extra conditional was worth it... but It seems likely

Data tested on

To test this I'm generating random strings. It's a simple algorithm where, with a probability of 9/10 I add another random uppercase letter, but always stopping at 50 charactors. I'm mentioning this because obviously the distribution of the data could impact the overall performance of a given algorithm. Note that this means functionally we're only actually using 26 of our 128 buckets. On the other hand, real strings are usually NOT evenly distributed, since languages carry heavy biases towards certain letters. This means my test is not exactly represenative, but I haven't given it a clear advantage either.

Conclusion

I can't say that this is a clear win for Radix Sort for sorting mixed-length strings. The temporary space issue can be non-trivial, and certainly time isn't always worth trading for space. We're using O(3N) additional space for this sort. That said, there are some obvious ways to reduce the space overhead if you need to, e.g. radix-sort smaller chunks of the array, then merge them. Use 32 bit instead of 64 bit pointers, or come up with a cuter radix-sort.

Note that my radix-sort was a mornings work to figure out the algorithm, write and validate an implementation, find a couple optomizations, and benchmark it. I wrote this post later. Oddly "inline" made a huge difference to gcc's runtime (it's needed due to loop unrolling for handling the A/B list cases). In any case, I've little down someone can beat my implementation, and maybe find something using a bit less space. I just wanted to prove it was viable, and more than competitive with comparison based sorts.

Median Find

2018-12-19

Similar to Radix Sort, I thought it might be interesting to see how worst-case linear time medianfind actually performed. Since the algorithm is identical to expected-case linear-time medianfind (usually called quickselect), except for the pivot selection, I elected to add a boolean to the template to switch between them (since it's in the template it'll get compiled out anyway). Before we go in to the results, here's a quick refresher on these algorithms:

Problem Statement

Imagine you have a sorted array. If you want the K'th largest element, you can simply look at the element in location K in the array. Comparison-based sorting an array takes O(Nlog(N)) time (strictly speaking the theoretical limit is log-star, but it doesn't really matter). What if we want to do this without sorting the array first?

Quick Select

Quick select chooses a pivot and runs through the array throwing elements in to 2 buckets... smaller and larger thanthe pivot. Then it looks the number of elements in the buckets to tell which one contains the k'th element, and recurses. We can prove we usually choose a good pivot and this is expected O(N) time. But it's worst-case is much worse.

Worst-case-linear Quick Select

What if we always chose the right pivot? Or at least... a good *enough* pivot. This is how we build our worst-case-linear quick select algorithm. It's a really cool trick, but it's been covered in many places. So if you want to know how it works you can check wikipedia, or this nice explanation .

Real World performance

All of that is great in theory, but what is the *actual* performance of these things... well, in a benchmark, but at least on a real computer.

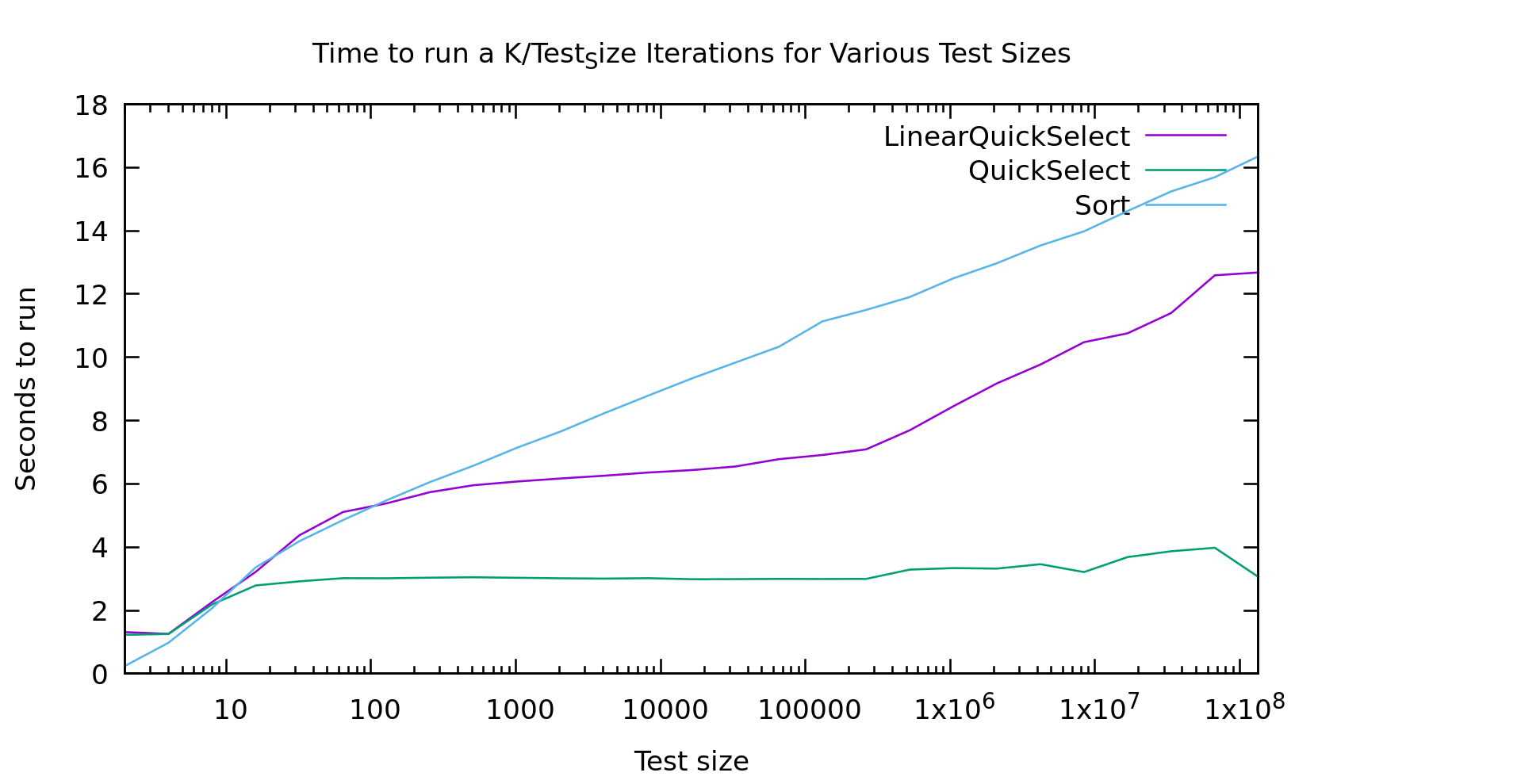
As usual I'm working on an array of test_size k/test_size times, so we work over the same number of array-cells at every point on the graph: small arrays many-times on the left, and large arrays fewer-times on the right.

For a while I was pretty upset about these results. The runtimes for "lineartime" quickselect look more like quicksort (the algorithm displayed as the "sort" line) then they do like basic quickselect. In short... that doesn't look linear at all. What the heck?

I must have a bug in my code right? This algorithm was proved linear by people much smarter than me. So, my first step was to double-check my code and make sure it was working (it wasn't, but the graph above is from after I fixed it). I double, triple, and quadrouple checked it. I wrote an extra unittest for the helper function that finds the pivot, to make sure it was returning a good pivot. Still, as you see above, the graph looked wrong.

I finally mentioned this to some friends and showed them the graph. Someone suggested I count the "operations" to see if they looked linear. I implemented my medianfind algorithm using a seperate index array. That way I could output the index of the k'th element in the *original* array. From there everything is done "in place" in that one index array. As a result, swapping two elements is my most common operation. That seemed like a pretty accurate represention of "operations". So, here's what that graph looks like.

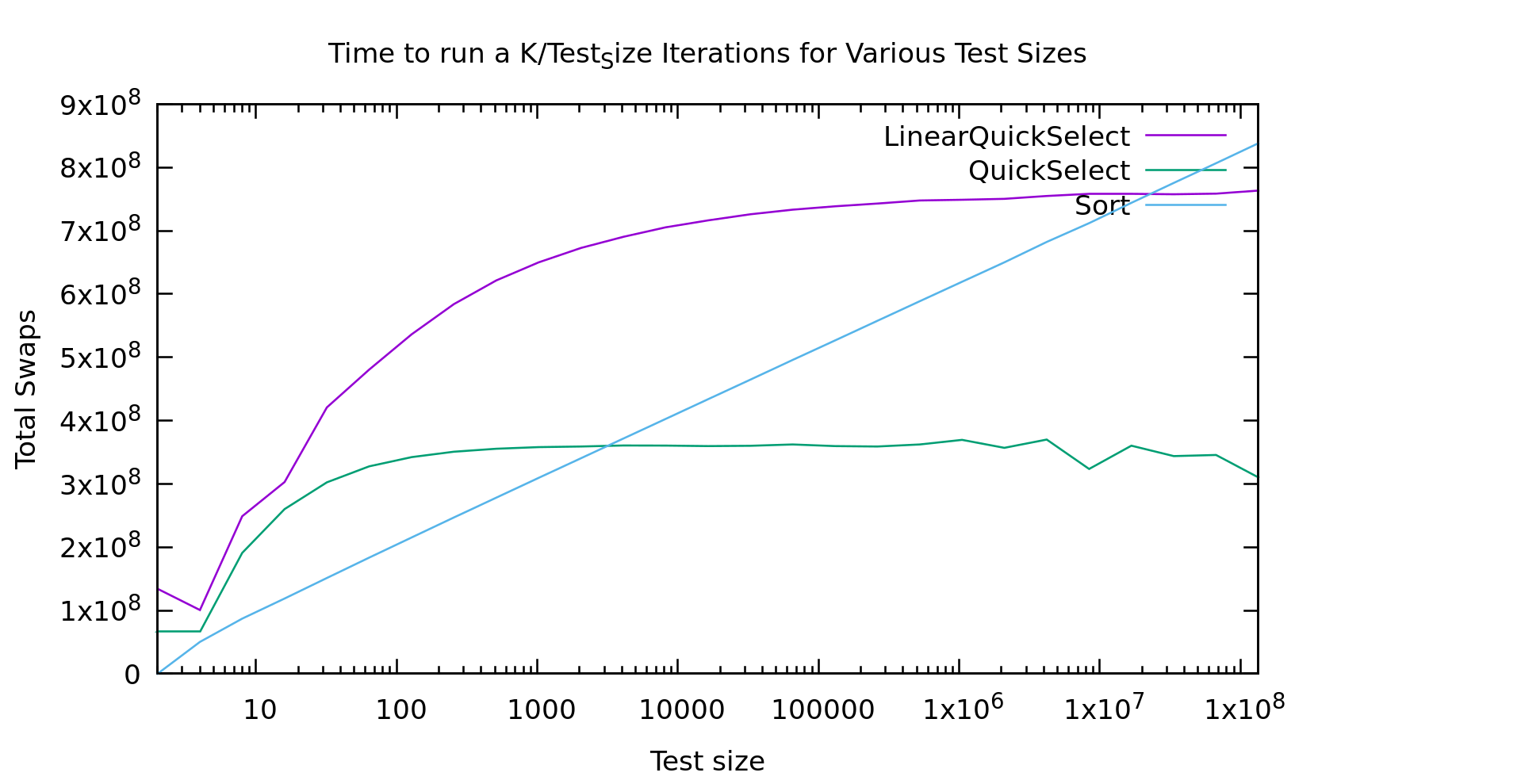
Now THAT look's a bit more linear! It's not exactly a flat line, but it looks asymptotic to a flat line, and thus classified as O(N). Cool... So, why doesn't the first graph look like this?

Real machines are weird. That index array I'm storing is HUGE. In fact, it's twice the size of the original array, because the original is uint32_t's and my index array is size_t's for correctness on really large datasets. The first bump is similar in both graphs, but then a little farther to the right in the time graph we see it go crazy... that is probably the algorithm starting to thrash the cache. Presumably if I made it big enough we'd see it go linear again. That said, if we go that large we're soon running on a NUMA machine, with even more layers of slowness, or hitting swap.

So, should you *ever* use guaranteed linear-time medianfind? Probably not. If there is a case it's vanishingly rare. It happens pivot-selection distributes well, so there's probably a use there? But, if you just used the "fastsort" we talked about in my last post you'd get even better performance, and it's still linear, AND it distributes well too! It's not comparison-based of course, but there are very few things that can't be radixed usefully with enough of them, and if you're stubborn enough about it.

Big O notation didn't end up proving all that useful to us in this case did it? Big O is usually a good indicator of what algorithm will be faster when run on large amounts of data. The problem is, what is large? Computers are finite, and sometimes "large" is so large that computers aren't that big, or their behavior changes at those sizes.

Fast Sort

2018-12-17

In my last post I was benchmarking various sorts against each other to test a couple of radix algorithms. https://blog.computersarehard.net/2018/12/sort-benchmarks-and-modern-processors.html . Radix Sort came out the clear winner for large data sizes (as we would expect), but that experiment left some questions.

In particular, on small arrays (less than ~100 elements in size), Radix Sort performed quite poorly. I posited a couple of theories. Maybe it's prefetching and branch prediction, or maybe it's all of the passes over the radix-array itself that costs more (as a friend of mine suggested). If the former is the main factor than we should see little performance difference as the radix-size changes. If the latter is the main factor then as the radix-size goes up our runtimes on these small arrays should shoot through the roof.

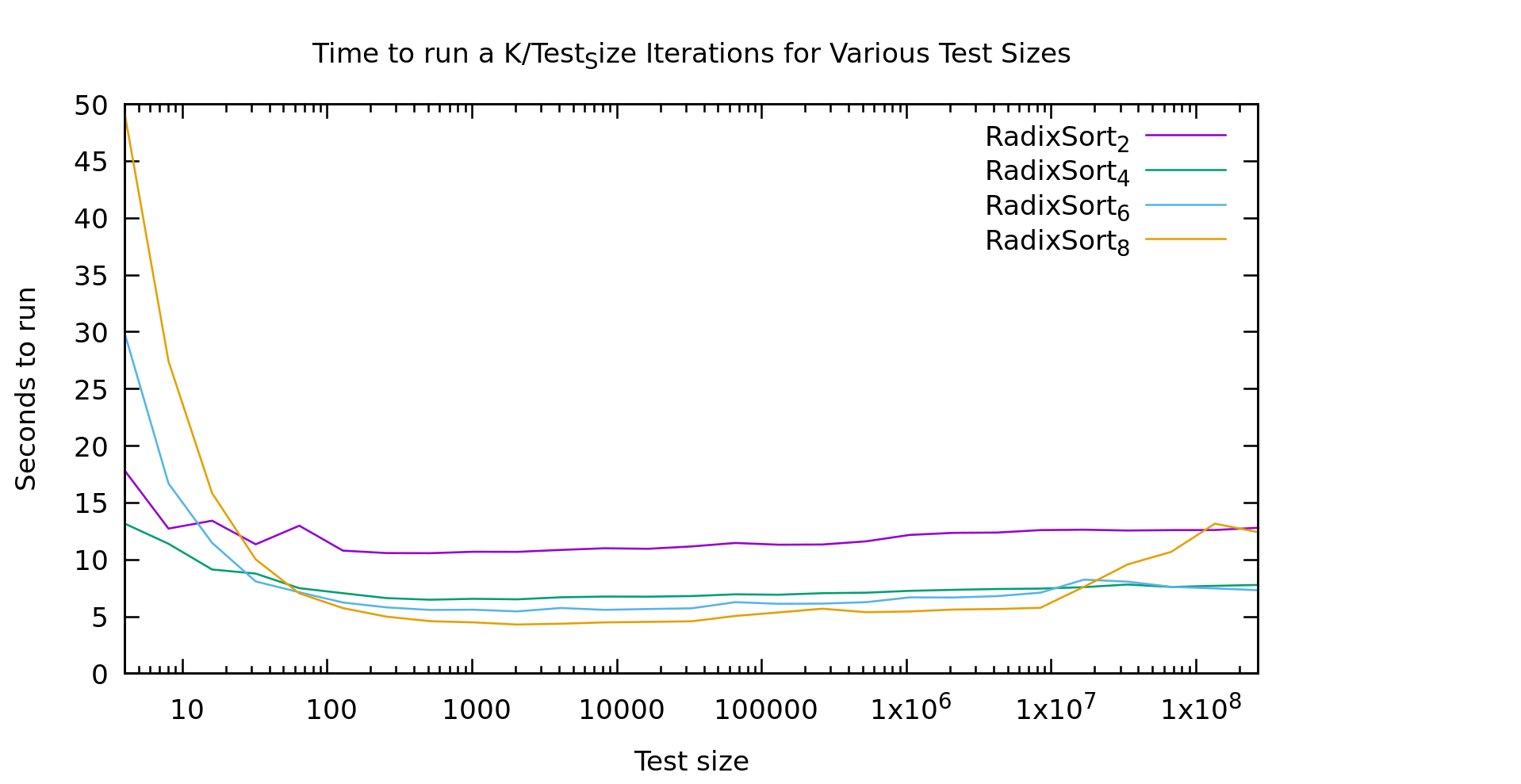
Radix Sort arity test results

As you'll recall from my last post, every point on this graph involves sorting the same number of elements. The X axis indicates the length N of the array sorted, but it is then sorted K times where N*K = a constnant. This way this graph shows nonlinearities in the algorithms as they change with N. The subscript for each algorithm is the number of *bits* in the radix, so the actual radix-size is 2^K (e.g. 256 for the yellow line). Note that the constant is not the same as my last post, so please don't cross-compare the graphs.

This graph gives us a pretty clear answer. Our slow performance on small arrays is definitely the radix array. With a radix of 256 it doesn't start to look linear until around 1000 elements, and doesn't beat a radix of 2 until ~20 elements.

You're probably wondering about the weirdness out on the right. Testing on any larger arrays gets somewhat time-consuming quickly. Logarithmic graphs are annoying that way. That said, I generated several graphs like this one, and all had similar artifacts towards the right, especially for larger radix sizes. But it looks pretty noisy overall. My current guess is caching behavior. The machine I'm testing on is far from sanitary, lots of other stuff is going on in the background. It could be that as radix sort uses nearly the entire cache it becomes highly sensitive to other workloads. A larger radix might have more opportunity for chunks of the radix array to get kicked out repeatedly and thus be more sensitive.

Mixed sort

We saw in my last post that radix sort is extremely valuable for larger data-sizes, in fact, it beat out eeverything else by around 40 elements. On the other hand, we also saw that it has pretty bad behavior on really small arrays. Those results were found with a radix size of 32 (or 5 bits, which would land between the blue and green lines on todays graph).

From this new experiment we see that there is a significant cost to larger radix sizes. For most uses on modern computers 256 integers is a non-issue memory-wise. But, with a large radix our performance is abysmal on really small arrays. A standard solution to this type of problem is to blend algorithms (this is frequently done with quicksort, using selection sort for extremely small arrays). Heapsort and mergesort both are stable sorts as well so they seem like good candidates. Lets see how they compare.

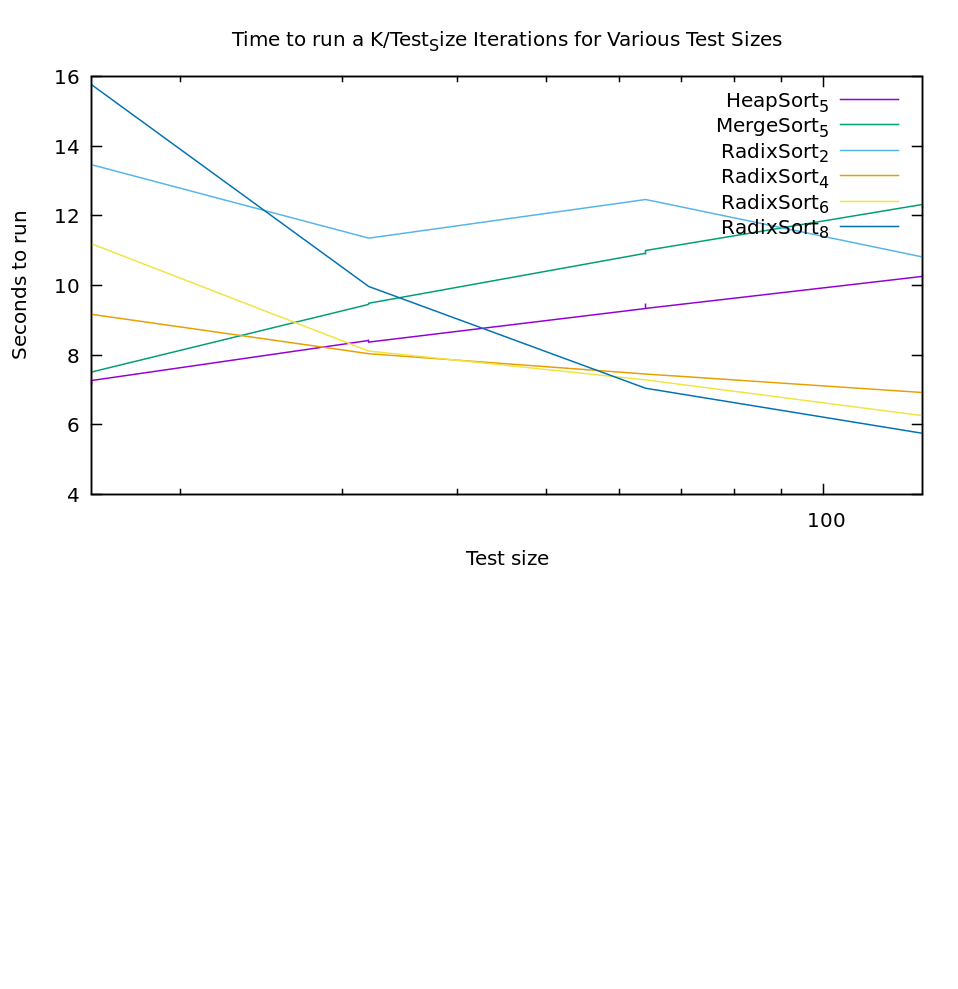
Radix sort arity test results

The graph is a bit ugly because I didn't do a ton of points, but the results are still pretty clear. If we just take the best algorithm at every point it looks like we should use heapsort <20, then radix sort with 4 bits up to 30, then radix sort with 6 bits up to 60, and then radix sort with 8 bits. No doubt if I tested larger radix sizes this trend would continue.

Of course, if our conditional choice gets to complex it's cost becomes a problem as well. To make radix sort fast it's compiled with the radix size as a template parameter, so each switch is going to tresh code cash, etc. If you're getting THAT picky you'll be benchmarking for your specific use-case anyway. So for general use I would propose that we keep it simple. Heapsort up to about 30, and then radix sort with 6 bits above that is a nice simple algorithm that gets us pretty close to our ideal speeds. It certainly wipes the floor with any other single algorithm. We'll call our new mixed algorithm fast sort.

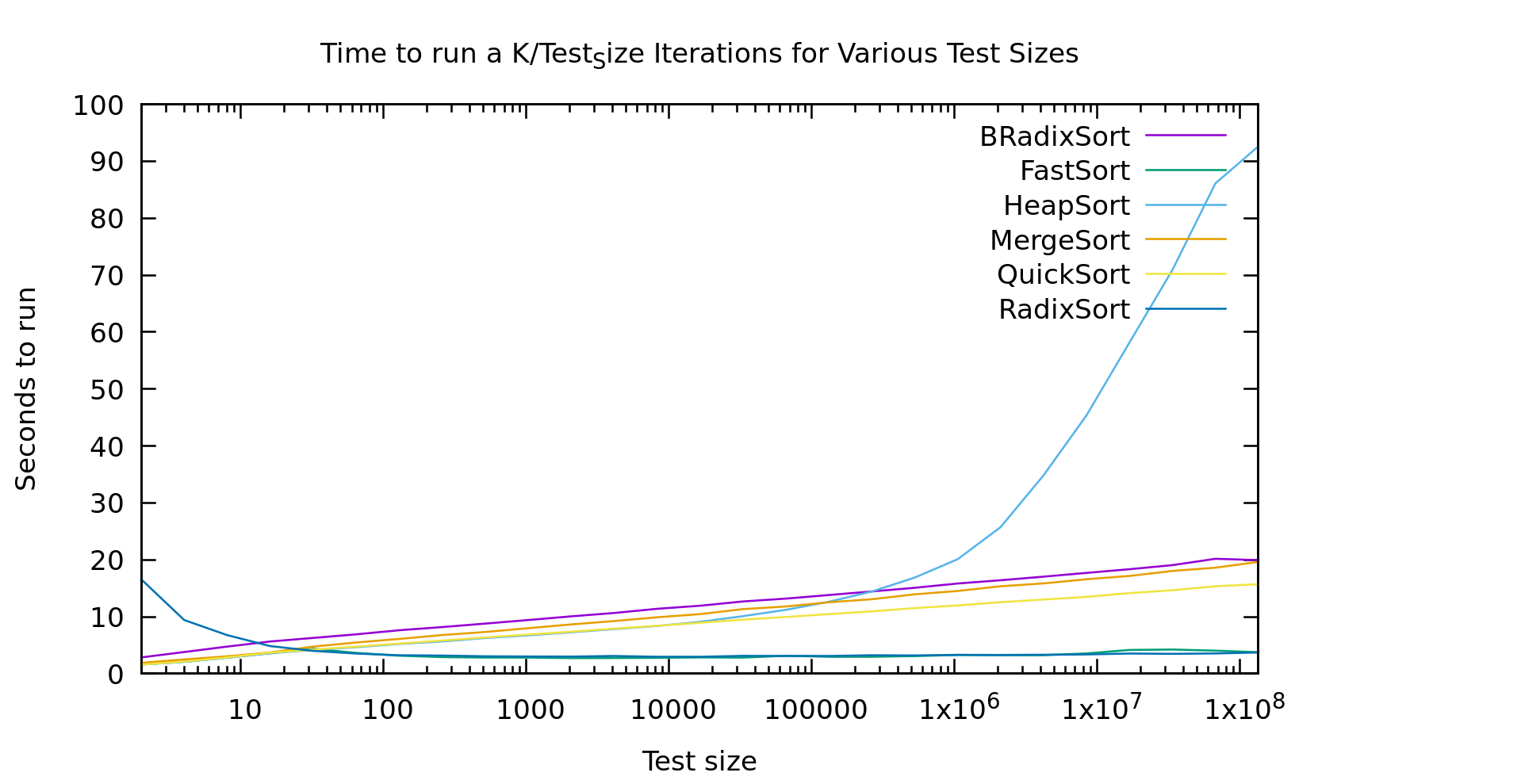
Radix sort arity test results

It's a little hard to see the green line that is fastsort, but that's because it performs exactly how we would hope, like heapsort up until 30, and then like radix sort with a 6 bit radix.

Conclusion

Discussions of sort speeds are usually theoretical (how many comparisons are being done). In reality, as we showed with AVL trees being just as fast or faster than Red Black trees, moves and cache behavior play at least as big of a role as comparison count. Most of the literature I've seen says heapsort is not a good choice for speed alone, while here we've found it to be a very good option for smaller arrays. Our final fast sort algorithm differs from anything you are likely to find in a textbook, yet is an extremely performant, and by happinstance stable, sorting algorithm.

There are of course caveats to these conclusions. As noted in earlier posts, these are my implementations, it's always possible (even probable) that I'm farther from the ideal implementation for one algorithm than another. Additionally our fast sort has one rather annoying property drastically limiting it's utility. Our radix algorithm has to work on the type being sorted. At the moment it's written for unsigned types, but it would have to be changed for signed types, strings, integral types larger than size_t, etc. With comparison-based sorts you can sort largest-to-smallest simply by swaping the comparitor. With radix sort (and thus fast sort) significantly less trivial adjustements have to be made to the sort itself if you don't want to have to reverse it in a seperate pass. In practice, these limitations are probably why radix sort gets so little attention despite it's obvious strengths. The details can't be abstracted away as cleanly as comparison based sorts.

Sort Benchmarks and Modern Processors

2018-12-13

A couple of days ago I realized I'd never actually sat down and written a Radix Sort. For the Computer Scientists among us, we spent a lot of time in school learning about various comparison based sorts (quick sort, selection sort, merge sort, etc.), and how they compare to the theoretical lower bound. Radix sort is mentioned as interesting in that, since it's not comparison based, it can beat those bounds. They vaguely explain it, and move on.

In practice MOST sorting in actual code is done using quick sort, due to it's average runtime. I've ranted on this blog before about average vs. worst-case, and how I think software engineers tend to greatly over-emphasis average case... but even putting that aside, take a look at this graph.

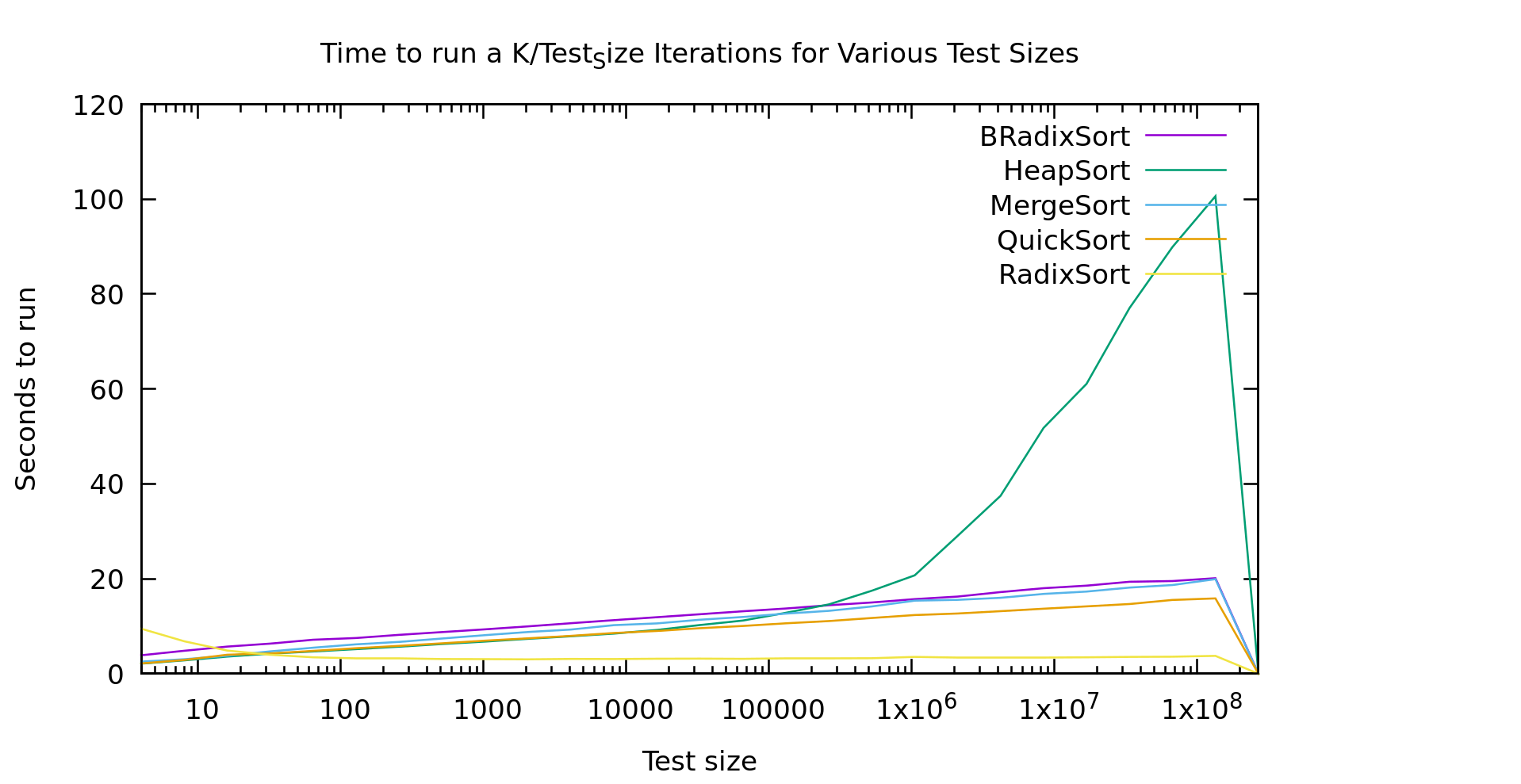
Runtims of various sorting algorithms

BRadixSort is a most-significant-bit first in-place binary radix sort. RadixSort is a least-significant-bit first radix sort using 32 buckets. Also, just for disclosure this is sorting unsigned 32 bit ints on my old Intel Core i7-4600U laptop.

I've shown graphs like this on this blog before, but I think I explained them poorly. Every point on this graph involves an algorithm running on the same TOTAL number of elements. The difference as you go right is that it's sorting larger and larger arrays, while doing it fewer and fewer times. This way the graph drops out the effects of just sorting more elements, and instead shows the non-linearities in varous algorithms as they work with larger and larger arrays.

Make sense?

Now. Most of these results are about what you'd expect if you've got a background in this field. Except three oddities.

Heap Sort

With heap Sort I'm I think this is related to cache sizes. We all know that quick sort and merge sort are preferred over heapsort due to constant factors right? Well sure, but here we see heap sort is actually faster than merge sort for smaller lists (this could actually potentially be useful, since it's also in-place and stable). I think the problem is that as heaps get bigger you completely lose adjascency between a node and it's children. This means basically every access is random, no prefetching and caching advantages. My machine has a 4MB cache. It falls apart just about the time it starts cache-thrashing, while other algorithms are taking advantage of prefetch logic by running liner through the data

Radix Sort

Radix Sort should take O(n*log(k)) where k is the largest element we're sorting. You can also think of log(k) as the number of bits in the elements we're sorting. This is of course completely linear in N, and the graph shows almost exactly that. Except that weird slope at the start.

That bump at the start has a couple possible causes. It could be branch prediction failing us horribly, or it could be walking that 32-bucket list twice. It might be interesting to try and pick it apart.

To explain why branchprediction makes sense. When we sort a tiny list over and over and over again, our algorithm isn't doing anything terribly predictable. So, very likely branch prediction *correctly* guesses that we'll loop basically every time, and never break the loop. If we then break that loop after only looking at 4 elements, we get a complete pipeline dump every 4 elements... ouch. Radix Sort scans both the data, and it's index array twice per pass. It does this for log(k)/buckets passes. But, each pass goes straight through list. This means LOTS of loops to mispredict, while on big lists prefetching logic knows *exactly* what we're doing, so it's able to pull in the data before we need it. Given no other factors slowing it down it actually gets faster on larger arrays, where prediction is basically perfect.

Binary Radix Sort

Binary radix is supposed to have the same time complexity as Radix Sort, but that graph doesn't look "linear in N' at all. If it was linear in N it would be a flat line like Radix Sort is. Here's my guess as to what's going on. It's true that Binary Radix Sort will take at MOST log_2(K) passes. But, that's a lot of passes. In fact, in practice log(K) is usually larger than log(N). After all, we usually work with numbers the same size or larger than the size of our address space right? Even if we limit K to 32 bits, it's still larger than most lists we'd sort on a single machine.

Binary Radix Sort is also capable of terminating early. Since it's recursive, at some point a sublist only has size 1 and there's no need to keep iterating through the bits at that point. This means the average runtime is actually more like N*min(log(N),log(K)). For every list in the graph shown here Log(N) < Log(K) so it's effectively an Nlog(N) algorithm. My guess is that if I did another 4 or so points we'd see that line go flat, but I'm just not sorting big enough arrays ('cause I don't want to wait that long).

Conclusion

There are several takeaways here:

One last note. I don't want to oversell my results. Please keep in mind that these are MY implementations. I may well be missing a tweak that would get a significant speedup somewhere. I spent a little time on RadixSort to get this performance. At first my constant factors were so bad it wouldn't have beaten anything until ~100k elements or so. Declaring constants as constants, replacing division ops with bit ops, etc. sped it up by around 5X. Micro-optomization is usually a waste of time, but here is where it can really pay off.

As always you can find this code on github https://github.com/multilinear/datastructures_C--11.git/ .