Fast Sort
2018-12-17
In my last post I was benchmarking various sorts against each other to test a couple of radix algorithms. https://blog.computersarehard.net/2018/12/sort-benchmarks-and-modern-processors.html . Radix Sort came out the clear winner for large data sizes (as we would expect), but that experiment left some questions.
In particular, on small arrays (less than ~100 elements in size), Radix Sort performed quite poorly. I posited a couple of theories. Maybe it's prefetching and branch prediction, or maybe it's all of the passes over the radix-array itself that costs more (as a friend of mine suggested). If the former is the main factor than we should see little performance difference as the radix-size changes. If the latter is the main factor then as the radix-size goes up our runtimes on these small arrays should shoot through the roof.
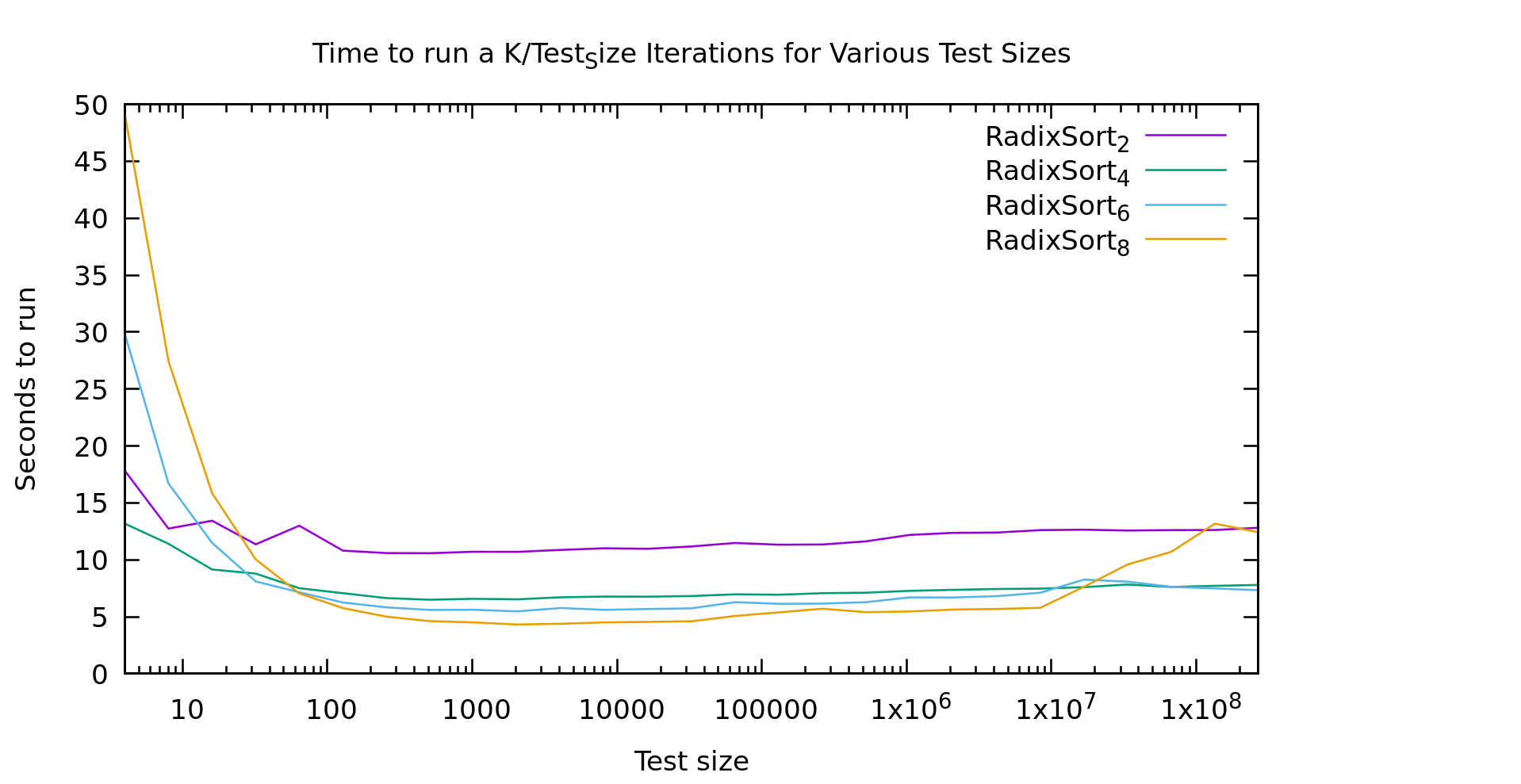
As you'll recall from my last post, every point on this graph involves sorting the same number of elements. The X axis indicates the length N of the array sorted, but it is then sorted K times where N*K = a constnant. This way this graph shows nonlinearities in the algorithms as they change with N. The subscript for each algorithm is the number of *bits* in the radix, so the actual radix-size is 2^K (e.g. 256 for the yellow line). Note that the constant is not the same as my last post, so please don't cross-compare the graphs.
This graph gives us a pretty clear answer. Our slow performance on small arrays is definitely the radix array. With a radix of 256 it doesn't start to look linear until around 1000 elements, and doesn't beat a radix of 2 until ~20 elements.
You're probably wondering about the weirdness out on the right. Testing on any larger arrays gets somewhat time-consuming quickly. Logarithmic graphs are annoying that way. That said, I generated several graphs like this one, and all had similar artifacts towards the right, especially for larger radix sizes. But it looks pretty noisy overall. My current guess is caching behavior. The machine I'm testing on is far from sanitary, lots of other stuff is going on in the background. It could be that as radix sort uses nearly the entire cache it becomes highly sensitive to other workloads. A larger radix might have more opportunity for chunks of the radix array to get kicked out repeatedly and thus be more sensitive.
Mixed sort
We saw in my last post that radix sort is extremely valuable for larger data-sizes, in fact, it beat out eeverything else by around 40 elements. On the other hand, we also saw that it has pretty bad behavior on really small arrays. Those results were found with a radix size of 32 (or 5 bits, which would land between the blue and green lines on todays graph).
From this new experiment we see that there is a significant cost to larger radix sizes. For most uses on modern computers 256 integers is a non-issue memory-wise. But, with a large radix our performance is abysmal on really small arrays. A standard solution to this type of problem is to blend algorithms (this is frequently done with quicksort, using selection sort for extremely small arrays). Heapsort and mergesort both are stable sorts as well so they seem like good candidates. Lets see how they compare.
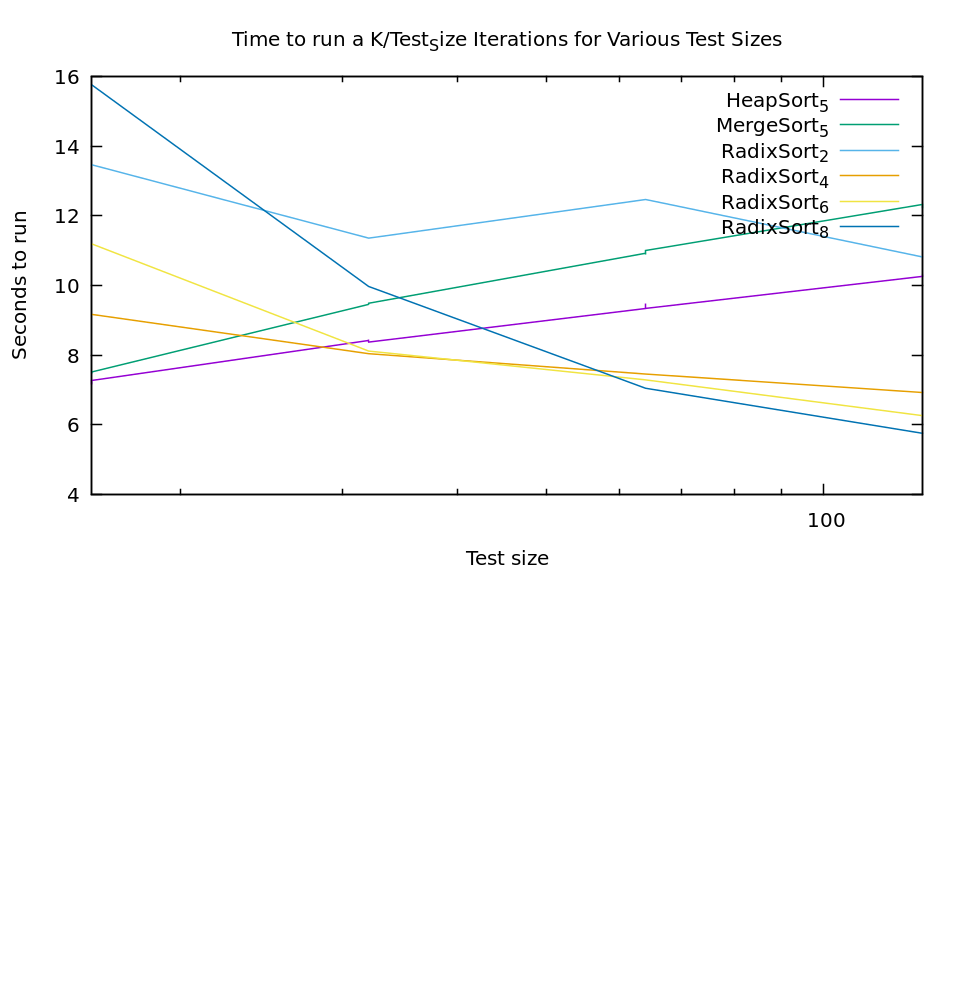
The graph is a bit ugly because I didn't do a ton of points, but the results are still pretty clear. If we just take the best algorithm at every point it looks like we should use heapsort <20, then radix sort with 4 bits up to 30, then radix sort with 6 bits up to 60, and then radix sort with 8 bits. No doubt if I tested larger radix sizes this trend would continue.
Of course, if our conditional choice gets to complex it's cost becomes a problem as well. To make radix sort fast it's compiled with the radix size as a template parameter, so each switch is going to tresh code cash, etc. If you're getting THAT picky you'll be benchmarking for your specific use-case anyway. So for general use I would propose that we keep it simple. Heapsort up to about 30, and then radix sort with 6 bits above that is a nice simple algorithm that gets us pretty close to our ideal speeds. It certainly wipes the floor with any other single algorithm. We'll call our new mixed algorithm fast sort.
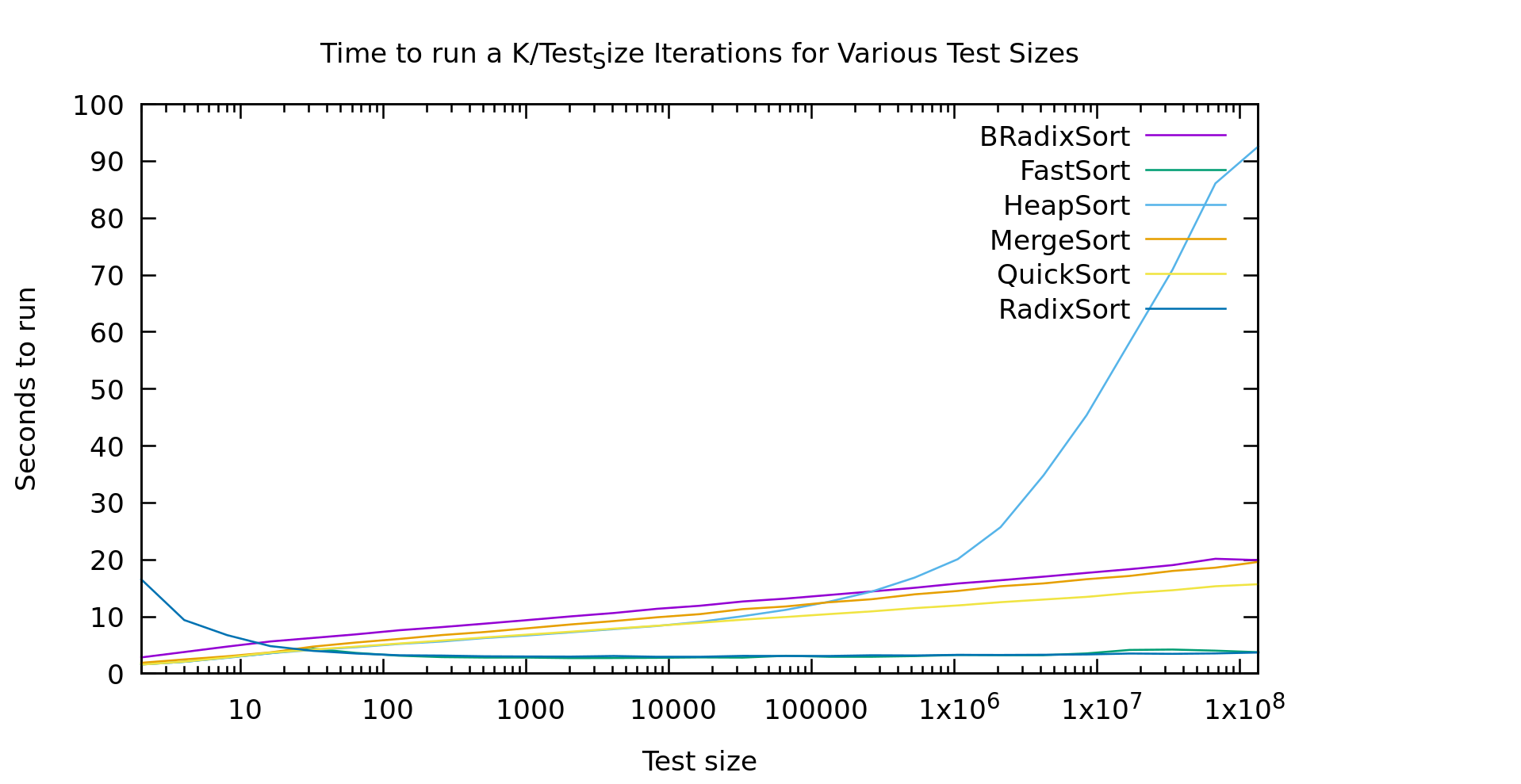
It's a little hard to see the green line that is fastsort, but that's because it performs exactly how we would hope, like heapsort up until 30, and then like radix sort with a 6 bit radix.
Conclusion
Discussions of sort speeds are usually theoretical (how many comparisons are being done). In reality, as we showed with AVL trees being just as fast or faster than Red Black trees, moves and cache behavior play at least as big of a role as comparison count. Most of the literature I've seen says heapsort is not a good choice for speed alone, while here we've found it to be a very good option for smaller arrays. Our final fast sort algorithm differs from anything you are likely to find in a textbook, yet is an extremely performant, and by happinstance stable, sorting algorithm.
There are of course caveats to these conclusions. As noted in earlier posts, these are my implementations, it's always possible (even probable) that I'm farther from the ideal implementation for one algorithm than another. Additionally our fast sort has one rather annoying property drastically limiting it's utility. Our radix algorithm has to work on the type being sorted. At the moment it's written for unsigned types, but it would have to be changed for signed types, strings, integral types larger than size_t, etc. With comparison-based sorts you can sort largest-to-smallest simply by swaping the comparitor. With radix sort (and thus fast sort) significantly less trivial adjustements have to be made to the sort itself if you don't want to have to reverse it in a seperate pass. In practice, these limitations are probably why radix sort gets so little attention despite it's obvious strengths. The details can't be abstracted away as cleanly as comparison based sorts.