String Sorts

2019-01-23

You'll recall in my recent post about Fast Sort we learned that Radix Sort is significantly faster at sorting 32 bit integers than normal comparison based sorts, particularly as the array gets large. A result every computer scientist knows theoretically, yet with median-find we saw how theoretical bounds don't always translate in practice.

Well, a friend asked me, what about sorting variable length strings? Does radix sort still beat comparison based sorts? It's a fair question so, I decided to take a shot at it. And here are my results:

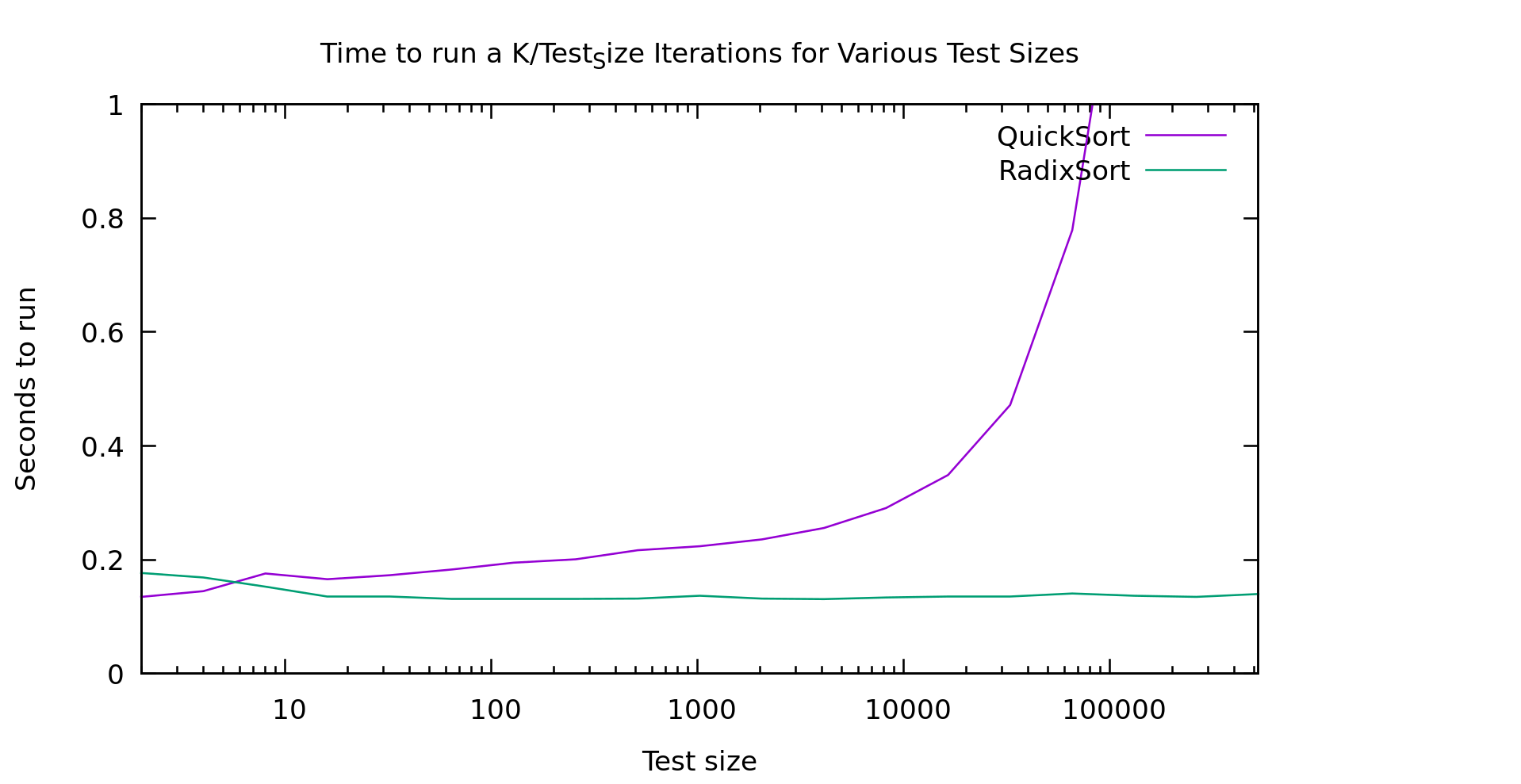
In my mind that graph is pretty clear, above 10 elements radixsort is clearly winning. Note that this is currently a 128 bit radix-sort that only handles ASCII... though I'm actually only feeding it uppercase strings currently. So, lets talk about how this algorithm works, because it's not an entirely trivial conversion of radixsort

String Radix Sort Algorithm

This is a little bit interesting. You may recall that there are two types of radix-sort. Least Significant Digit first, and Most Signicant Digit first. These are referred to as LSD and MSD. My binary radix sort from earlier benchmarks was an example of an MSD sort, and the one I just referred to as "radix sort" is an LSD sort. LSD sorts are preferred generally because they are stable, simplier to implement, require less temp space AND are generally more performant.

There's just one problem. With variable length strings, LSD sorts don't work very well. We'd have to spend a lot of time scanning over the array just looking for the longest array so we can compute what counts as the smallest significant bit. Remember that in lexicographic ordering it slike all the strings are left justified. The left-most charactor in each string is equivelent in precidence, not the rightmost.

MSD sorts, must be recursive in nature. That is, they need to work on only the sublist we sorted in to a certain bucket so far. I'm going to call this sublist a "slice". To keep our temporary space vaguely in order I'm using a total of 5 lists.

Here's the algorithm. Start by looking at the first bytes of the strings. Look in slice list A, and get the next slice. Bucket everything in this slice. Each of these buckets (if non-empty) becomes a new slice, so write strings back out to string list B, and write the index of end each slice in to string list B. Swap lists A and B, move to the next byte, and do it again. We terminate when for each slice it's either of length 1, or we run out of bytes. To see the full implementation take a look at string_sort.h in my github repo .

Conveniently, they way my algorithm works it is in fact stable. We walk the items in order, bin them in order, then put them in the new list still in order. If they are equal there is no point where they'd get swapped.

It's a LOT of temporary space, which is kind of ugly, but it's pretty performant as you saw above. Another optomization I haven't tried is short-circuiting slices of length 1. We should be able to trivially copy these over and skip all the hashing work. Testing would be required to see if the extra conditional was worth it... but It seems likely

Data tested on

To test this I'm generating random strings. It's a simple algorithm where, with a probability of 9/10 I add another random uppercase letter, but always stopping at 50 charactors. I'm mentioning this because obviously the distribution of the data could impact the overall performance of a given algorithm. Note that this means functionally we're only actually using 26 of our 128 buckets. On the other hand, real strings are usually NOT evenly distributed, since languages carry heavy biases towards certain letters. This means my test is not exactly represenative, but I haven't given it a clear advantage either.

Conclusion

I can't say that this is a clear win for Radix Sort for sorting mixed-length strings. The temporary space issue can be non-trivial, and certainly time isn't always worth trading for space. We're using O(3N) additional space for this sort. That said, there are some obvious ways to reduce the space overhead if you need to, e.g. radix-sort smaller chunks of the array, then merge them. Use 32 bit instead of 64 bit pointers, or come up with a cuter radix-sort.

Note that my radix-sort was a mornings work to figure out the algorithm, write and validate an implementation, find a couple optomizations, and benchmark it. I wrote this post later. Oddly "inline" made a huge difference to gcc's runtime (it's needed due to loop unrolling for handling the A/B list cases). In any case, I've little down someone can beat my implementation, and maybe find something using a bit less space. I just wanted to prove it was viable, and more than competitive with comparison based sorts.