Designing for correctness
2025-07-27
There aren't nearly enough abstract discussions about how to design code for correctness, but there are even fewer that talk about concrete examples. Having just posted Tasx, I thought it might be interesting to use it as an example of how to think about designing for correctness. I'm sure I didn't do everything right, and I'd love for people to tell me how I'm wrong so I can make it better, but a lot of thought went into how to avoid bugs. So lets talk about some principles and how I applied them.
Make failures obvious
One big trick to designing for correctness is to minimize the chance that mistakes and failures go unnoticed. The first method is the classic "fail early and fail often". I'm not saying to litter your code with pointless asserts. Rather I mean that if the logic for a section of code assumes something is true, but won't crash if it's false, make it crash if it's false. On the other hand, if it would already naturally reliably crash (like a null pointer dereference) don't add unnecessary code. This is actually a basic design principle underlying rust. It tries to crash the minute something is weird and not let it propagate forwards in your program. That's what unwrap (and what you replace it with) is all about. This has the additional advantage of keeping crashes local rather than letting them propagate, which makes debugging far far easier.
A less discussed method to make failures more obvious though is to minimize branching and special case code. Usually when bugs sneak through you're QA process (whether your QA process is an entire QA team, some unittests, or just running the software by hand and seeing if it works), it's something *unusual* that happened. Bugs are almost always in some bit of code that isn't usually exercised. Yes, you can try and write tests to test every corner case, but you can also design your code to minimize corner cases in the first place.
In Tasx I started with a simple data model. I get CalDav task structures from the kitchen-fridge crate, and I put them in a list (the list is dictated somewhat by GTK). When a mutation occurs I changed the tasks stored in the list. I also had a version sitting in kitchen-fridge's cache. So, when I mutate the one in the list I have to also mutate the one in cache. It's a little messy, but not too big of a deal.
But, then I needed another window to edit the tasks. So, I added one (The details window that pops up when you click a More button). The toolkits I'm using run the other window in it's own thread. I could put my list behind a mutex, but I'll get into why I didn't in a bit. Instead, I copied the entire Task structure into the other thread. Now edits can come from two places and go to 3 places. This is getting problematic. It'd be easy to have an edit somehow change one version but miss another, and I had several such bugs. That was no good. So, next I switched to sending the entire task around. This let me centralize changes. I could edit the local copy of the task then send it elsewhere and let it propogate. I still have propagation logic for each starting source, but it's still not too bad.
Then, it got worse again. To do nested tasks I needed to understand child/parent relationships while sorting the list. To avoid ludicrous data duplication I needed the data stored in a dictionary. I couldn't abide duplicating the data, so I pulled the tasks out of the list, moved them into the hashmap, and put just the necessary data for display in the list (and a UID so I know what needs changing). Now I'm back to bespoke editing for data in the list again! Around the same time I added support for the "Description" field, which could easily be a short essay, and it's updated with each keypress for UX reasons. So, I might be copying this data all over the place every time I send a task around. Even worse I was tracking each tasks "children", and editing the child list was a mess. What if two threads needed to change the child list at the same time? If I just overwrite the task one of the edits will gets stomped. It was time for another redesign.
So, I designed a "TaskChange" structure. This structure would encode just the fields that get changed. For the "children" property I could now have a "delta" concept that adds or removes a child. This makes mutation order way less important.
Now all my mutations run through 3 functions, add, delete, and change. Changes can come from anywhere in the program and get propagated by exactly the same code. Display of a mutation is not done locally (okay, there's one corner-case, but you get the idea), it always propagates the same way. This means I only have to get it right once, and what I see when I make a change is going to be the data everywhere. If I have a stupid bug like the code is missing to apply the change to the "Description" field I'll know it because my edit to the description field won't show up in the UI.
Reducing corner cases
I said I would come back to why I didn't use a central data store and mutex it. The first is simply that I want a responsive UI and mutexes are not a great way to get that. Relm4 and GTK have asynchronous APIs so by default you get a responsive UI as long as you don't screw it up. But, I could just make sure I never hold a mutex for very long right?
But there's another downside. Race conditions are the worst kind of corner cases. They are just the right combination of random and consistent such that they are completely impossible to fully test. Such race conditions are global properties of the code. Every time I mutate data I have to make sure to do it in the right order. I need to take this mutex before that one. If in one place it's the other order, I could deadlock. If in one place I mutate the data in the wrong order between/outside mutexes some other code could see an inconsistent state. It's a lot to think about every time you touch that structure. I probably would've ended up copying data out of the structure just to avoid races or holding a mutex too long. Sometimes it's worth all of that when you really need that common data store, but I really didn't. In my case the kitchen-fridge cache, the hashmap, the list, and the details window can all have different versions of the data for a short time, I don't care. As long as things eventually line up (in a few milliseconds) the user won't even notice. That's pretty easy to do with messages particularly since all mutations go through a central point, mutations can't "cross". Once again that centralized mutation design is helping us out.
Conclusion
When thinking about design people often talk about readability vs. performance. Those are important aspects, and a lot has been written about how readability contributes to correctness. In fact, many classic coding rules like avoiding duplication are intended to contribute to correctness. Test driven design is often discussed as another method to improve correctness. But, what I'm proposing is a more of a mindset, a wholistic view where you design to try and minimize the very corners bugs can hide in. In my case this is how I cheat having to write real tests, but in a big project this is how you reduce your test surface area and bring your test matrix down to something that is *possible*. If you then take the design into account when designing how to test you can write a heck of a lot fewer tests (and save on infrastructure costs as well).
I'm sure Tasx will have bugs found in it, but between rust, and these design choices, I've drastically reduced the types of bugs that could slip through even my very rudimentary QA process. If it's not good enough, I might have to actually go write a few tests.
Lastly, remember that Tasx is open source. If you want to make this more concrete you can go read the code, including the history and all of my stupid mistakes: https://codeberg.org/multilinear/tasx .
Tasx a Todo app in Rust
2025-07-26
Tasx is a CalDav to do application written in Rust, supporting offline use, and targeting Linux as it's primary platform. The intention is to be a standalone application good for desktops, laptops, tablets and smartphones. I wrote it and am releasing it to "public beta". This means it should be fully functional, but being only person who's tested it I'm too nervous to call it "stable" yet. The UI looks really simple which is good! It is really simple! But it's fully featured supporting nested tasks, hiding subtasks, moving tasks into and out of parent tasks, manual ordering via drag-n-drop, stacked orderings, hiding and showing completed tasks, notes, edits to not require pressing enter (creating new stuff does). We have keyboard shortcuts, a notes section, etc. (I probably should grab a screenshot of the window that pops up when you hit "more"). The goal is to be obvious and simple, but correct and support everything.
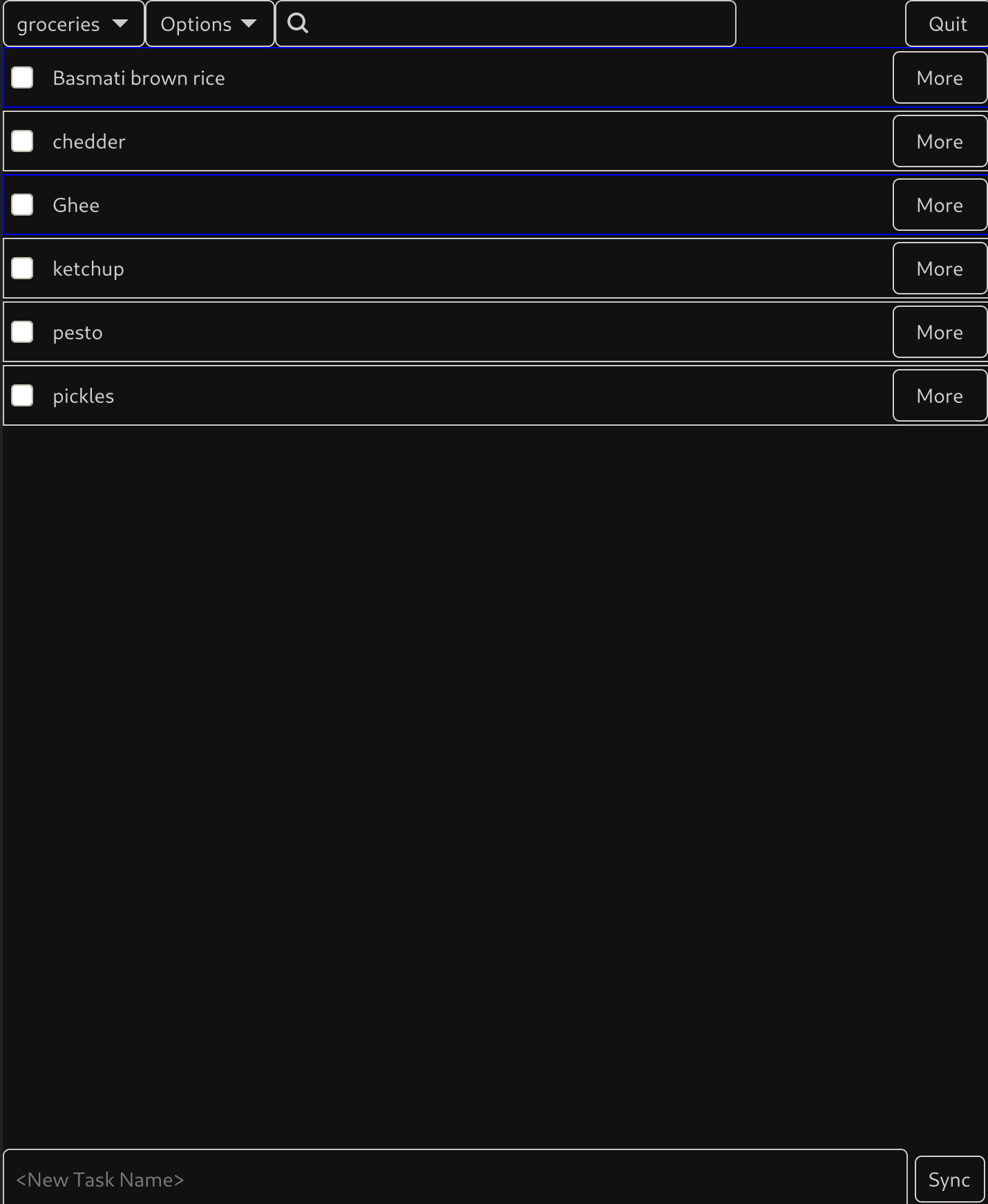
If you're interested, check out the project on codeberg: https://codeberg.org/multilinear/tasx . I've written some fairly simple instructions for installing, but you do need GTK4 and Cargo/rustc.
Now, I thought I'd tell a bit of the story of how and why I wrote this.
I've mentioned previously on this blog that I have a Pinephone. I got it running Gentoo, and that was cool, but it turned out I don't need a palmtop anymore. It was exactly what I wanted for decades, but my life is different now. But, I'm ged up with corporate crud and Google Android is now developed closed-source and only released open after the fact going even farther from FOSS. My wife and I make heavy use of the FOSS Tasks.org app on Android for things like shopping lists. Tasks.org syncs via the CalDav protocol through my self-hosted NextCloud server. After digging around a while I didn't see any suitable replacements for a Linux phone I came up empty. Gnome Tasks was missing several features I wanted, and syncs through the enlightenment backend which together is both under and over engineered for my use-case. Thunderbird is similarly a huge application and missing features for Task management. So, I decided to write what I wanted to exist.
I've done most of my professional work in C++, but have a programming language theory background from college. Anyone who's done a lot of C/C++ knows the downfalls and how hard it can be to get a project stable. To explain: consider how python make it super easy to get over the hump of getting *something* that sort-of works. But C/C++ is far easier to get from there to something relatively stable. Rust is like this difference but in the exponent. It makes it much easier than any other language I've used to get a stable, trustworthy, and secure application. I'm not promising Tasx won't have bugs, but I am saying it has far fewer than it would had I spent the same effort in C or C++ with none of the performance downsides of languages like Java. On top of that, as a network application Tasx sits on a security boundary. While I didn't write any network code myself, I have more faith in the libraries I'm using in Rust than I would on most C++ libs for the same reasons. Specifically, CalDav is XML, and XML is a minefield of exactly the sorts of problems C/C++ is known for.
Having selected Rust to code this application, the next step is picking a GUI toolkit. My goal was native, lightweight, and relatively shallow and straightfoward dependencies. Given this I was skeptical of a lot of the Rust GUI libraries that advertise being able to run as a webpage or similar. They might be good, but didn't seem like where I should start. Looking around GTK4 seemed the best fit. GTK4 has wide usage already so most users will already have it installed, so I'm not generally adding more libs to the system. The GTK4 Rust crate is also one of the only toolkits that's officially stable. So, I decided that was the way to go. After some digging I learned that with the combination of GTK and Rust's data models the best approach is to use channels to get the data "out" of GTKs concept of a view to where you could process it. This makes for a lot of boilerplate. Relm4 is a Rust crate that wraps up most of that boilerplate, but still allows direct access to all the GTK APIs, so that seemed like a good bet.
Then what about the networking and CalDav side? The last thing I want to do is write an XML library, or even a CalDav library if I can avoid it. Digging through Rust crates online I eventully found Kitchen-Fridge, which is a caching caldav client library that allows you to access and modify the cache offline as well, making it perfect for my needs. It took me a bit to realize the stable version was broken, but the unstable version did what I needed. A To Do app is a demo example for both GTK-rs and Relm4. Between those, this should be a trivial app to write... right?
Of course not. There's a huge gap between a demo and a product. I wrote down a list of features I wanted and just started adding them. As an experienced developer anything algorithmic I find quick and fun, the difficult part is figuring out APIs. Drag and drop for reordering took me a particularly long time. It works well in practice, but a GTK expert could no doubt make it cleaner. I wanted the app to feel snappy, so synchronization needed to run in another thread and most of the app is asynchronous. I went through several internal data models trying to work out the best way to synchronize data across threads before settling on the "change" model I'm using now (which minimizes data copies while centralizing mutations to keep bugs obvious).
This app is (currently) entirely single author, so I'm the only one to yell at if you hate it.
I tried it on my Pinephone running Phosh Mobian Trixie and it works and feels pretty nice at various scalings. I also tested the install process on that platform. I did try it on my wife's Debian Bookwork laptop running Cinnamon as well, but it has too old a version of Rustc/Cargo, but it works fine if you build the binary elsewhere and copy it over.
I don't use my Pinephone regularly, and I probably still won't, but this is a step in that direction for me and hopefully for the wider Linux on Smartphone ecosystem. In the meantime I use do it daily on my laptop and it's been excellent there. I hope you use it too.
Now that I've learned some GTK and such I want to write a standalone Calendar app for Linux as well so I can ditch thunderbird on desktop, but that's going to be a little while.
Cellphone Followup
2024-07-28
A while back I wrote about running Gentoo on the Pinephone Pro . I was pretty excited about it and I still think it's an actually usable system. So, did I go use it?
No, I didn't.
I realized after I built that system that I built it for a younger me. It was exactly what I wanted when I was 14 and still what I wanted in to my early 30s, but it's not actually what I want now. Back then I was a mobile person. I worked in labs. I flew regularly. I backpacked. I lived in a truck for several years. For all of that I wanted a real computer that fit in my pocket even if it was a little hard to use. I've tried a myriad of devices to fill this role. From the HP Jornada to phone cases with kickstands and external keyboards. I used devices like this somewhat regularly to write blog posts, email people, or even write software. When I lived in a truck such devices were also useful because they draw less power. I had ssh working on my kindle and used it a few times to do things I cared about. That use-case is what I built for on the pinephone pro, and it worked!
Now I live in a house. I am usually here and usually have a laptop at my disposal. My mobile device's primary functions are showing me maps and where I am on them, storing grocery lists, and communicating with my wife. Secondary functions include reading error codes from my car, playing music, letting me access information via webbrowser, email, photos, and as an e-reader. None of these are power-user/real-computer things. They are standard boring modern "phone" things. I'm not sshing, or writing long-form emails, or any of that stuff on my mobile device. In fact, I gave my wife my folding keyboard so she could use it when she travels.
So, I finally folded and got a "normal" smart phone, a pixel 6a. But, I still care about privacy and security, so I'm not about to just go run stock android. I'm currently running LineageOS, though next time I'll probably install GrapheneOS or Calyx. I'd installed LineageOS on my wife's phone previously when it dropped out of support, and I'd run rooted CyanogenMod before that, so this wasn't entirely new. What is new is that I'm finally not using Google services, because I simply don't need it.
I've been using that configuration for a couple of years now, and it's fit my usecase very well. I run k-9 mail for my email, fluffy-chat for matrix chat, molly for signal, fennec for my browser, OsmAnd for maps, NextPush for push notifications, Syncopoli for syncing music and Auxio to play it, Tasks for grocery list and such, tuner for tuning my guitar, KeepassDX for passwords, AndrOBD to debug my car, stock calendar and contacts.
I can also run the few closed-source things I still need. My fiber install has been stalled for months so I'm still on starlink and need the starlink app. I use OnX Hunt for property boundaries when wandering my forest because I've yet to find an open source alternative. I use Waze when I need specific real-time map features road closures, or better address lookup than OsmAnd can provide.
Overall this solution has been satisficing. It's more of a compromise and I'm not entirely happy about being on the cell network all the time and thus having my location traced, logged, and likely sold to 3'rd parties. On the other hand, it actually meets my daily needs and is still an order of magnitude better for privacy than a default android phone.
Solar Inverter Monitoring
2024-07-18
I installed a hybrid solar inverter and battery bank in my home a little while ago. I have panels on the way right now, but in the meantime I've had the inverter up and running as a whole-house UPS for a little while.
But, what does this have to do with computer hackery and comp-sci theory you ask? It's a fair question and I'm getting there. The SolArk, like most modern pieces of technical hardware, comes complete with a bunch of web integration. You plug in a little WiFi dongle and your data gets whisked off to a datacenter somewhere, where you can have the privilege of accessing it in some limited ways through a mediocre web interface and maybe some annoying REST APIS. I found this unsatisfactory for a number of reasons
- This is a hybrid solar inverter. Part of it's purpose is to power my home when grid power is down, which means, network communication might also be down. When I *most* want to see my data, I'm likely to not have communication.
- I want to access the data MY way, with my own scripts
- No-one but me needs to ever see it.
- It offends my sensibilities. Why is my data traveling all over the world when I only need or want it *here*.
- I don't trust IOT devices to have properly implemented security, because, they usually don't, so it's having this thing on my network is a security hole in my network.
And my solution was this
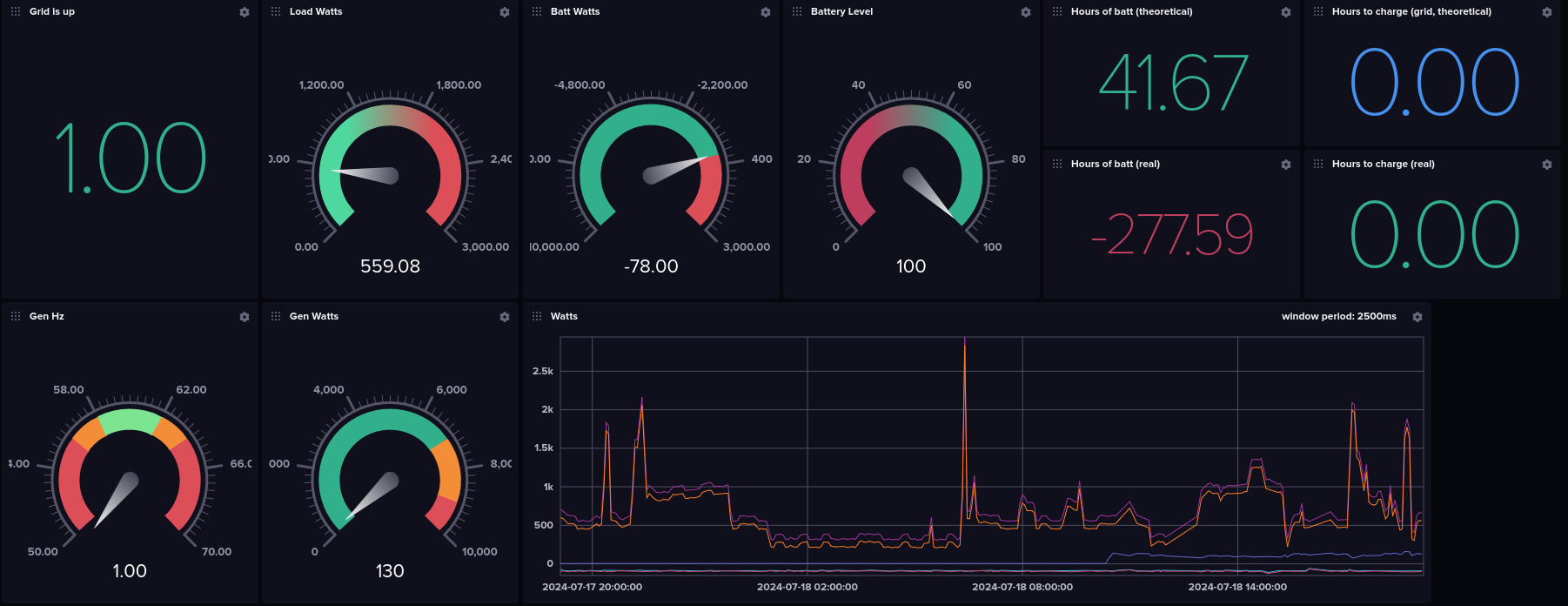
First Steps
Pulling the data
But, the Solark fit my needs really well otherwise. So, rather than whine and whinge about it I decided to see what would be required to get the data off the device myself. I thought this would be a HUGE project, but as it turns out it wasn't at all. With a little searching online I found that the solark speaks modbus, and they actually published a spec for it . You can talk to the solark over a couple of different interfaces, but I already had a USB->RS232 adapter lying around, so I plugged it in and after playing around in python for a little while I started getting data.
Logging the data
I already had an IoTaWatt for monitoring power usage in my home. It's both open-source hardware and software, and it supports pushing the resulting data into InfluxDB. So, I'm also running InfluxDB on my home server. I actually used this set of tooling to help understand my power usage so I could properly size my solar build. Anyway, the point is I already have my power usage data in InfluxDB, and it'd be great to have my solar data in the same place. So I dug up a python library for influxDB and pretty soon I had my data streaming into InfluxDB... pretty cool.
Alerting the data
Well, that's all well and good, but I have to keep looking at my dashboards. If my power goes out my WHOLE HOUSE is backed up, so there's no obvious way to even know that my power is out. That's... not great. So, I want my wife and I to get notifications somehow. I asked my wife what she'd prefer and she it should just come to our cellphones. That made sense to me. The two of us currently use the matrix chat protocol to talk to each other wherever we are. Though, we currently use an external server for this (so it won't work our communications are out), it's fully open source and I can set up and run my own server, and probably will.
So, I dug up a matrix library. This turned out to be the hardest part, especially as the first library I tried wasn't flexible enough for what I needed. I ended up moving the entire program from asynchronous, to synchronous, and then back to asynchronous again, but I eventually got it working. And, here's the result
Getting Serious
I ran that program for maybe a month and eventually got it largely working, but still felt... sketchy. In python it's hard to have any confidence in codepaths that aren't actively tested. This program is really just communication at it's heart, which means a lot of possible points of failure. But, then I hurt my foot and had a lot of time to kill, and I'd been meaning to learn rust, so I rewrote the whole thing
This was my first real project in rust and it didn't disappoint. As I expected the type safety gave me far more trust in corner cases that I'm unlikely to bother testing. The "?" operator is a really convenient cross of exceptions and error return codes. I found that it helped me think about all the error cases without adding much complexity to the code. That, combined with the single mutable reference restrictions in rust did make some functional idioms harder to use, and I definitely tried a few cute "Build up all the futures and then run them" sorts of tricks that didn't work. But, all in all it's better than any other language I've tried for this type of code.
Final notes
The final result is one of the few personal projects I could see someone else actually wanting to run, with proper configuration options and files, and all of that jazz. The real takeaway here though is that I had a problem, and I solved it, and while not *easy*, it wasn't that hard either. I run my new monitor on system startup, so I don't have to think about it and hopefully it will just hum away logging what's going on and letting me know when something interesting happens.
If you're in the space you may wonder why I didn't integrate with Home Assistant. The answer is that Home Assistant is cool and open source and stuff but... not really up my ally. It feels large and bloated, it's nearly impossible to run without virtualisation, it's intended for people who like clicky-button interfaces rather than configuration-as-code, and I just don't need it. Having Home Assistant play middleman would, if anything, obscure the simplicity of what's going on here, adding layers of abstraction, conversion, protocols, DSLs that would be in my way.
FOLLOWUP
I've been running this software and indeed it is more stable than my python version. It took me about 3 days to write. By the time I had all the features and it felt like it was working, it was working. After that I had one bug in room joining that was a pure logic error on my part, and that was it. I added a few more design improvements and adjustable values, but it was a drastically different experience from the weeks of bugs still popping up occasionally in the python version.
I noticed that the development process in rust is very different. Before retiring recently my job was coding in C++. I'm not an "outline" kind of person. I'll start in one of two places. If I'm worried that something is going to be too hard or impossible, I'll start there to gain clarity on that piece of the system and "de-risk" the project. If I'm not worried and I'm fuzzy on the overarching design I'll start with the part I do know so I can build outwards from there. Both of these approaches work well in the languages I've used the most professionally: C++, python, javascript, and a number of DSLs, but rust has it's own ideas.
In rust most of your time is spent trying to get the program to compile. I'm a newbie so this is extra true for me, but I have enough experience in languages like SML and Ocaml to have a good idea that this remains true even for fairly skilled developers. In fact, arguing with the compiler constantly is the point of rust. You spend your time trying to get it to compile, possibly re-writing it a couple of times as your realize your way of thinking of the problem isn't compatible with rust's, instead of spending time debugging. The compiler is telling you "no" and forcing you to work through things you wouldn't realize until testing in other languages. That's a wonderful property. There's a side-effect though where you quickly find you're constantly asking "will the compiler let me do that". To answer that you need to be able to ask, and for to ask it the rest of your program needs to be valid. So, there's this strong incentive to keep the whole thing compilable most of the time as you develop. For this reason I quickly found myself switching to an outline style of programming. I'd write a "dummy" for a function or a struct so I could write outer code first, then go write the inner code later. This isn't a bad thing, but it's the first time I've run into a language who's design so strongly encourages one approach over another.
Linux Software I use
2023-03-24
I find that a large percentage of my time "tweaking" linux is spent searching for software that I like. I've slowly built up a toolset that's lightweight and stable, and does the things that I generally need to do - and I thought that *maybe* someone else would find this list useful too. I am sure there are better ways to do some things, but I'm pretty happy with most of how my setup works.
Rather than try and come up with a list of programs I use, Gentoo already has this list sitting around for me in the form of the world file. For non-gentoo folks, the world file is a list of every package I explicitly installed, and doesn't include dependencies. So it's pretty much everything I use. I did drop some stuff from the list that's just boring, like fonts and git.
One reason this list might be interesting to someone is that this configuration is 100% wayland. I'm not running X or XWayland. So if you're looking for a wayland solution to something, this list might be a helpful list. Another reason is that I strongly dislike heavyweight software. I will generally choose the lightest-weight option available. I do still have thunderbird on this list, I'm not saying I always use the most minimal option. Sometimes I just want to look at a darn graphical calendar, but the bias in this list is clear.
Lastly you may notice that my configuration isn't over-engineered, in fact it's very under-engineerd. I have hard-coded paths just written into scripts. This is partly because this really is what I run, not some cleaned up configuration I created for posting. It's also because I don't like over-engineering. As is I can fix this stuff really easily. My notifications aren't working? Oh yeah, that wav file doesn't exist, eh, just find a new one. It's no harder to modify notifications.py than it is to modify the config that calls it. I'm probably erring too far on the side of lazyness, but hey, it works.
I've dropped some of the less interesting entries from the world file, things like git, fonts, etc.
- app-admin/keepassxc - password DB
- app-editors/vim - preferred editor
- app-laptop/laptop-mode-tools - preferred power managemenet
- app-misc/evtest - for UI tweaking, tests for events
- app-misc/jq - for commandline fiddling with json
- app-misc/khal - commandline calendar
- app-misc/khard - commandline contacts
- app-misc/ranger - commandline file browser
- app-misc/rdfind - find duplicate files
- app-misc/screen - useful for ssh access mostly
- app-office/abiword - reading microsoft .doc files
- app-office/gnumeric - spreadsheets
- app-portage/cpuid2cpuflags - identify flags for compiling
- app-portage/eix - find packages to install
- app-portage/genlop - examine build speeds and such
- app-portage/pfl - find what packages owns a file
- app-shells/gentoo-bashcomp - bach completion is nice
- app-text/antiword - make .doc files text files
- app-text/calibre - ereader (with DeDRM ability)
- app-text/xournalpp - PDF reader/editor
- dev-python/vdirsyncer - syncs data for khal,khard, and todo
- games-strategy/wesnoth - a fun game when I'm bored
- gnome-extra/nm-applet - network control
- gui-apps/clipman - better copy/paste semantics
- gui-apps/foot - terminal, I use the client/server mode, because it saves ram
- gui-apps/nwg-launchers - a nice app-grid, mostly used on my phone
- gui-apps/swaybg - set sway background
- gui-apps/swayidle - lock sway
- gui-apps/swaylock - lock sway
- gui-apps/tiramisu - notification middle-ware, I use a python script to take the output
- gui-apps/waybar - a taskbar, tray works where swaybar tray doesn't (in gentoo add the tray use flag)
- gui-apps/wlr-randr - change display settings
- gui-apps/wofi - another menu program, used for power menu on my phone
- gui-wm/sway - WM
- mail-client/mutt - email
- mail-client/thunderbird - gui email + calendar + rss reader, sometimes guis are nice
- media-gfx/geeqie - image library viewing
- media-gfx/imagemagick - image conversion
- media-libs/libsixel - allow w3m to show images in foot
- media-sound/abcde - rip CD music (I have a USB drive for this).
- media-sound/clementine - music player
- media-sound/fmit - guitar tuner
- media-sound/lingot - another guitar tuner I'm trying
- media-sound/pavucontrol - volume control
- media-video/mpv - video player
- media-video/pipewire - sound daemon
- media-video/vlc - old video player I'm moving off of
- net-fs/sshfs - to mount my servers FS if I want
- net-im/nheko - matrix chat client with E2EE
- net-irc/irssi - IRC client
- net-mail/grepmail - for looking through old mail archives
- net-misc/networkmanager - networking (matches nm-applet)
- net-misc/nextcloud-client - file sync
- net-p2p/qbittorrent - download stuff
- net-voip/linphone-desktop - SIP client
- net-vpn/wireguard-tools - VPN to server
- net-wireless/bluez-tools - bluetoothctl to manage bluetooth
- net-wireless/iw - wireless management
- net-wireless/kismet - wireless debugging
- sci-visualization/gnuplot - making graphs
- sys-apps/ripgrep - fast grep
- sys-power/acpi - get battery state
- sys-power/cpupower - CPU frequency scaling
- sys-power/hibernate-script - hibernation
- sys-process/iotop - IO load
- sys-process/lsof - find programs with open files
- www-client/chromium-bin - spare browser (when firefox fails to work)
- www-client/firefox - primary browser (I secure this one)
- www-client/w3m - console browser, and viewer for mutt
- www-misc/kiwix-desktop - wikipedia offline
- x11-misc/gmrun - app launcher
Not every piece of software I use is in the portage package system (or maybe it is but I haven't got searching for the overlay). I should probably write ebuilds for these and be all cool and Gentooy, but I haven't.
- itd - for syncing my pinetime watch
- todoman - for managing tasks (synced by vdirsyncer)
- gauth - a little TOTP tool written in go, haven't fully moved to keepassxc
Then I run a few things on my server:
- Nextcloud - for calendar, tasks, and contacts
- Nextcloud news app - for reading news
- Dovecot+fetchmail - pop email from gmail and serve it
- dnsmasq - to redirect my domain internally
But... how do you configure sway you ask? Never fear, here's my sway and waybar configs from my laptop. It's a pretty vanilla config, not much to see here. The notification bits are probably the most interesting
- waybar config waybar styling
- sway config Note: this is from my laptop and written for keepassxc to be the secrets provider (which I don't actually recommend). I'm using gnome-keyring as a secrets provider on my phone, and using systemd there. I also have some extra input/output statements to rotate the display and set up the pinephone keyboard. On openRC I start this with `exec dbus-run-session sway`, on systemd it's just `exec sway`.
- notifications.py is a python script that processes the output of tiramisu and dumps the result to an ephemral foot terminal. This is how I do notifications. The reason I do it this way is so I can make a sound when I get a message in nheko, so I don't accidentally ignore my S.O. This script just hard codes that to an "ugg" sound from wesnoth. Any old wav file will do. Note that foot is started with a special flag so sway can decorate it differently, and let it float.
Then a couple of short scripts I'll just post inline. The volume script is interesting because it changes ALL the pulseaudio volumes. This means shortcuts using it that get attached to e.g. the volume buttons on my phone, work when using plug-in headphones, a bluetooth speaker, USB headphones, or the built-in speaker. I've tried a lot of scripts over the years and this works the best so far. It DOES occasionally cause a weird jump in the settings if something else touched a volume, but I prefer everything to just adjust together for simplicity
volume
change=0
device=alsa_output.pci-0000_00_1f.3.analog-stereo
cur_vol=$(pactl get-sink-volume ${device} | awk '/front-left:/{gsub("%",""); print $5}')
new_vol=$((cur_vol + ${change}))
echo $new_vol
pactl list sinks | awk '/Name:/{print $2}' |
while read SINK; do
pactl set-sink-volume $SINK ${new_vol}%
done
lcd_brightness
#!/bin/bash
v=$(cat /sys/class/backlight/intel_backlight/brightness)
expr $v + $1 >> /sys/class/backlight/intel_backlight/brightness
It's possible to get w3m to display images in foot, even over ssh, which is pretty cool. I can run mutt on my server (I have it both places) and view images in an email if I want! This took a lot of poking around the internet, digging through configs, and guessing to figure out - and I've not seen anyone mention it anywhere, so I'm going to add it here. To convince w3m to display images in foot select "img2sixel" for the "inline image display method". For that to work img2sixel needs to be installed, which is part of libsixel in Gentoo. I have w3m-0.5.3_p20230121 built with imlib, gpm, ssl, and unicode use flags. I also have fbcon set, but I'm 95% sure it's not needed. As long as the terminal supports sixel (a format for displaying images in terminal emulator) it'll work. If it's working w3m www.google.com will display the google logo as an image.